今回は単語分散表現という機械に言語を認識させるうえで重要な技術について解説します。
結構難しくて理解に苦しみました、、、
単語分散表現とは
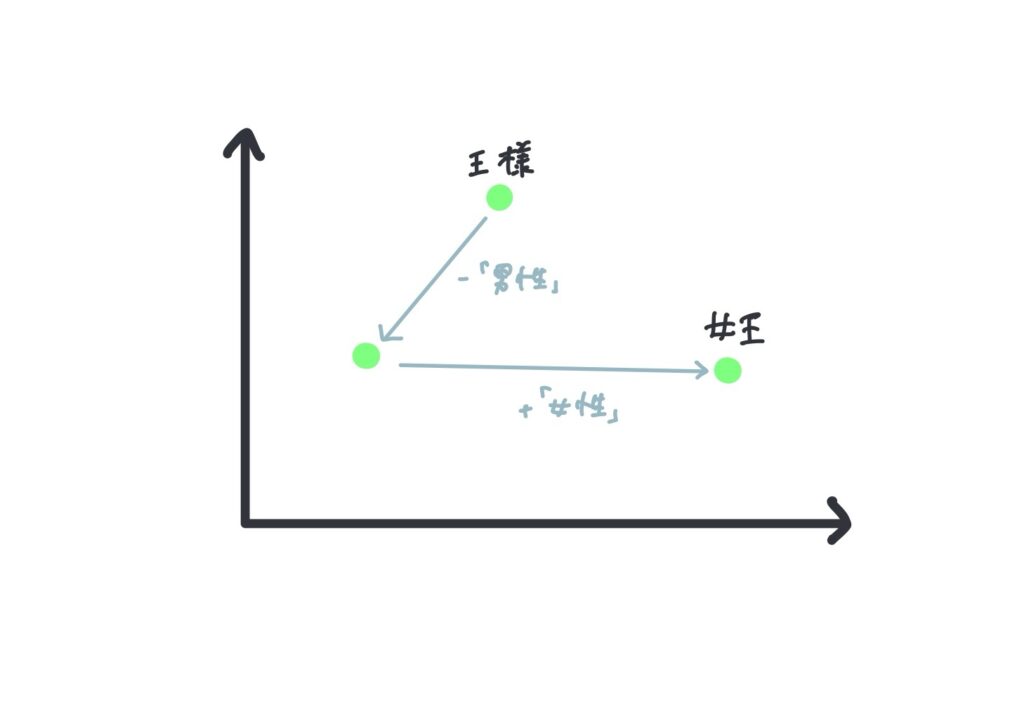
単語分散表現とは、単語の意味を低次元の実数値ベクトルで表現する技術です。これにより、単語間の意味的な類似性を数値的に計算できます。例えば、「王様」から「男性」を引いて「女性」を足すと「女王」が得られるような計算が可能です。
具体的にはOne-hot表現とは異なり低次元の実数地ベクトルを用いて単語を表現します。例えば下記のように単語をベクトル表現すると
| 単語 | ベクトル |
|---|---|
| リンゴ | [0.8, 0.6, 0.1] |
| オレンジ | [0.7, 0.7, 0.1] |
| 筆箱 | [0.1, 0.2, 0.9] |
リンゴとオレンジの類似度の方が、オレンジと筆箱の類似度よりも高くなります。
このように適切なベクトルを設定することで機械が単語の意味を認識できるようにしようとするのが単語分散表現です。
単語分散表現の基本的な考え方
単語分散表現の基本的な考え方は分布仮説というものです。これは単語の意味は、その単語が出現する文脈(周囲の単語)によって決まるという考え方です。例えば、「犬」という単語は「ペット」や「散歩」といった単語と一緒に使われることが多い。また、「猫」という単語も「ペット」などと一緒に使われることが多い。それらを学習した結果「犬」と「猫」は同じペットのような意味を持っていると機会に学習させることができます。
Skip-gramについて
Skip-gramとは単語分散表現を学習するモデルの一つです。Skip-gramの学習は教師あり学習で行い、入力としてある単語を出力としてその周辺語を与えます。その結果ある単語に対する周辺語の出現確率を学習することができます。
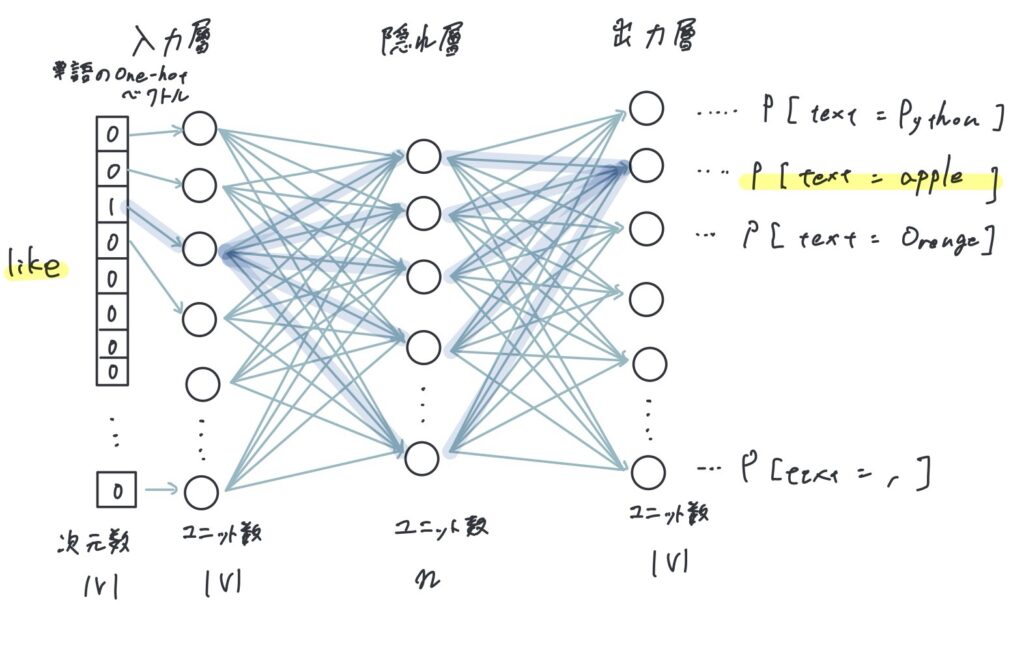
入力層
Skip-gramの入力層は単語を固定長で表したベクトルを与えます。固定長のベクトルとは、要素数や長さが一定のベクトルのことを指します。
単語を固定長で表すためにSkip-gramではone-hotベクトルを利用します。またこの時、ベクトルの次元数はボキャブラリの数Vに等しくなります。
- One-hotエンコーディング:
- 入力単語は、ボキャブラリ内の単語数と同じ長さのベクトルに変換されます。このベクトルは、入力単語に対応する位置に1を持ち、他の位置には0を持つ「one-hotベクトル」で表現されます。
- 例えば、ボキャブラリが
["I", "like", "apples"]で、入力単語が “like” の場合、one-hotベクトルは[0, 1, 0]となります。
隠れ層
隠れ層では与えられたone-hotベクトルに重みを掛けます。重みは行列Wで表され、行列のサイズは、ボキャブラリ数をm=|V|、隠れ層のユニット数をnとすると(m, n)とあらわされます。
- 重み行列との積:
- 入力層のone-hotベクトルは、重み行列 (W) と掛け合わされます。重み行列 (W) は、ボキャブラリサイズ(例えば10,000)と隠れ層の次元数(例えば300)の行列です。
- この計算により、one-hotベクトルの1に対応する行が抽出され、その行が隠れ層の出力となります。つまり、one-hotベクトルが
[0, 1, 0]の場合、重み行列の2行目が隠れ層の出力となります。
例えば、ボキャブラリが ["I", "like", "apples"] で、隠れ層の次元数が2の場合、重み行列 (W) は次のようになります:
\begin{equation}W = \begin{pmatrix}
0.1 & 0.3 \\
0.2 & 0.4 \\
0.5 & 0.7
\end{pmatrix}\end{equation}
入力単語が “like” の場合、one-hotベクトルは [0, 1, 0] です。このベクトルと重み行列 (W) の積を計算すると、隠れ層の出力は [0.2, 0.4] となります。
このようにして、Skip-gramモデルは入力単語を隠れ層のベクトルに変換し、そのベクトルを使って周辺単語を予測します。
出力層
出力層の役割は、隠れ層からの入力(単語ベクトル)を基に、周辺の単語を予測することです。具体的には、隠れ層からの単語ベクトルを使って、ボキャブラリ内の各単語が周辺語である確率を計算します。
出力層では、隠れ層から得られた入力単語の分散表現と、ボキャブラリ内の各単語の分散表現との内積を計算します。この内積は、入力単語と各単語の類似度を示します。
- 隠れ層からの入力:
隠れ層で得られた入力単語の分散表現(ベクトル)を$$\mathbf{v}_{\text{input}}$$とします。 - 出力層での内積計算:
ボキャブラリ内の各単語の分散表現を$$\mathbf{v}_{\text{context}}$$とします。
入力単語と周辺単語の分散表現の内積を計算します\begin{equation}\mathbf{v}{\text{input}}\cdot\mathbf{v}{\text{context}}\end{equation} - ソフトマックス関数:
内積の結果をソフトマックス関数に入力し、各単語が周辺語である確率を計算します:\begin{equation}P(\text{context word}|\text{input word}) = \frac{\exp(\mathbf{v}{\text{input}} \cdot \mathbf{v}{\text{context}})}{\sum_{i=1}^{V} \exp(\mathbf{v}{\text{input}} \cdot \mathbf{v}{i})}\end{equation}ここで、$$V$$はボキャブラリのサイズです。
例えば、入力単語が「eat」で、その分散表現が$$\mathbf{v}{\text{eat}}$$、周辺語「apple」の分散表現が$$\mathbf{v}{\text{apple}}$$だとします。出力層では、$$\mathbf{v}{\text{eat}} \cdot \mathbf{v}{\text{apple}}$$の内積を計算し、その結果をソフトマックス関数に入力して「apple」が周辺語である確率を求めます。
この内積が大きいほど、入力単語と周辺語の意味的な関連性が高いことを示します。
このように単語の重みベクトル同士の内積を計算しているとみなすこともできます。それを出力層でソフトマックス関数を当てて、確率を出します。
つまり、ここでの学習とは入力単語とその周辺単語の内積がしっかりと大きくなるように調整していくとなります。
単語分散表現のまとめ
ここまで学んだ内容を改めてまとめてみます。
- 単語分散表現とは単語同士の関係性を数値で表すこと
- Skip-gramでは入力単語からその周辺単語の出現確率を計算できる
- 入力層では入力単語をone-hotベクトルで表現し、隠れ層に渡す
- 隠れ層ではone-hotベクトルに重みを掛けて出力層に渡す。この時渡される値は入力単語に対応する重みのベクトルが渡される(one-hotベクトルでは入力単語以外の値が0だから)
- 隠れ層からのベクトルにsoftmax関数を割り当てて、周辺単語の出現確率を計算し出力する。
- 教師あり学習なので正しい確率が得られるまで隠れ層の重みを更新し、結果として重要なのはその隠れ層で掛ける重みを学習すること
- ここでの学習は教師あり学習が用いられ、学習の結果得られるのは次元数V×隠れ層のユニット数Nからできる重みを学習できる
計算量を減らす工夫(ネガティブサンプリング)
上記で学んだことをそのまま計算するとソフトマックス関数を当てる際にボキャブラリの数|V|の回数分繰り返すことになってしまいます。ボキャブラリの数は10の4乗以上になることが多いためこのままではモデルの計算に莫大な時間がかかってしまいます。
そのため、ネガティブサンプリングという手法を使って計算量を減らします。これは、(like, apple)など単語の出現確率としてあり得るものには1の教師データをラベリングしそうでない(i, apple)のようなあり得ないペアには0のラベリングをします。
こういったデータセットを用いることによってあり得ないペアに関する計算を除外することができ計算量を減らすことができます。
次の記事では実際に実装を行っていきます。
この記事は下記の書籍を参考にしています。


コメント